О сигналах и спектрах (окончание)

Вышеприведённую формулу обычно записывают следующим образом:

Ряд Фурье

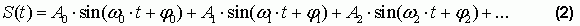
где

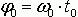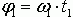и т.д. – назвали фазами синусоид. Фазы, таким образом, это всего-навсего лишь другая форма представления моментов времени в которые нужно нажать соответствующие клавиши нашего синтезатора – только и всего. Такова уж сложившаяся традиция в математике. Набор коэффициентов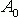

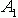, ... носит название амплитудного спектра, а коэффициентов

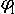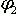, ... носит название фазового спектра. Таким образом, подобрав нужным образом коэффициенты амплитудного и фазового спектров мы сможем добиться того, что сумма справа в формуле (2) будет равна нужному нам сигналу S(t) слева. То есть из простейших “сигналов-кирпичиков” (синусоид) мы можем собрать любой сигнал. Вопрос лишь в том, чтобы подобрать нужным образом коэффициенты амплитудного и фазового спектров. Если нам известен сигнал S(t) который мы хотим “сыграть” на нашем синтезаторе, то есть специальные формулы по которым можно вычислить все коэффициенты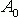

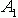, и т.д., а так же все коэффициенты

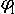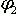и т.д. Это освобождает нас от подбора этих самых коэффициентов вручную “на слух”, “методом тыка” с целью добиться равенства выражения справа (в формуле (2)) сигналу слева (сигналу S(t)). Повторюсь: если S(t) задан, то по специальным формулам мы легко вычислим амплитудные и фазовые коэффициенты (соответственно силу нажатия и время задержки момента нажатия на каждую клавишу) необходимые для генерирования данного сигнала на нашем синтезаторе. Эти формулы и есть суть преобразования Фурье. А спектральное представление сигнала в свою очередь – это описание сигнала S(t) в виде набора коэффициентов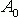

, ...,

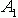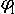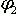, ... . Ведь зная эти коэффициенты мы всегда по ф-ле (2) легко можем восстановить S(t), а это означает, что эти коэффициенты есть полноправные представители сигнала S(t). На рис.17 представлен вид проигрывателя Windows Media при проигрывании музыки и здесь как раз в виде столбиков те самые коэффициенты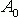

, ... амплитудного спектра звуков данной мелодии.

Амплитудный спектр

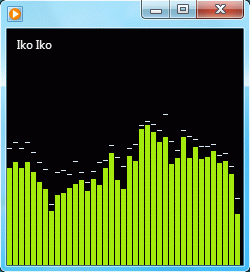
рис.17

Хорошо, скажут мне, преобразование Фурье – это суть синтез из простейших сигналов более сложных и любой сигнал можно заменить набором коэффициентов

, ...,

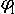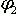, ... . Но для чего всё это? Что это нам даёт? И как это применяется в технике?
Прежде всего, спектральные представления применяются в технике передачи сигналов, сообщений, т.е. в технике связи. Например, всё это служит для оценки качества каналов связи. Допустим, нам предоставили для тестирования некий канал связи и просят ответить на вопрос – пригоден ли данный канал для передачи речевых сообщений. То есть будет ли по такому каналу проходить сигнал в виде голоса любого человека без искажений? Можно конечно набрать огромное количество людей, заставить произнести их огромное количество слов и фраз с разными интонациями, пропустить всё это через исследуемый нами канал и то, что получается на его выходе сравнить с тем, что было на входе. Если форма колебаний на выходе канала та же, что и на его входе, то канал пропускает сигналы без искажений. Однако вариант с привлечением огромного количества людей слишком затратен и мы всё равно не сможем получить все возможные голоса людей, произносящих в наш канал все возможные слова и фразы, а значит наверняка не можем уверено сказать, что, например, нет таких голосов и фраз, которые наш канал не исказил бы. А вместе с тем хотелось бы знать наверняка. Так вот спектральный подход позволяет обойти все эти сложности. Мы с вами уже знаем, что с точки зрения спектрального представления голос любого человека это некие сложные колебания, которые можно составить из простых колебаний-синусоид – главное чтобы в нашем распоряжении был набор этих самых синусоид с частотами от 50 до 10000 Гц. Так вот, если мы выясним, что все эти синусоиды проходят по тестируемому нами каналу без искажений, а также, что к сумме синусоид на входе канала не добавляются какие-либо сторонние синусоиды на его выходе, то смело можем делать вывод, что и любая сумма этих синусоид (с любыми коэффициентами

, ...,

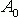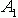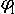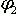, ...) пройдя через канал не изменится, а значит и сигнал S(t), состоящий их этих синусоид, который и есть голос любого человека, так же не изменится. А проверить, как проходят 9950 синусоид по каналу гораздо легче, чем заставить произнести в этот канал разные фразы с разными интонациями миллионы и миллиарды людей. Тем более, что часто не требуется пропускать через канал все эти наши 9950 синусоид по отдельности. Существуют методики, где нужно лишь несколько раз пропустить через канал специальные тестовые сигналы и мы будем точно знать проходят ли эти 9950 синусоид по каналу успешно или с искажениями. В приведённом примере наш речевой сигнал состоит из синусоид чьи частоты лежат в пределах от 50 до 10000 Гц. Этот диапазон частот называют шириной спектра сигнала. Если канал пропускает без искажений все синусоиды с частотами из данного диапазона, то говорят, что ширина полосы пропускания канала достаточна для пропускания данного сигнала с данной шириной спектра. Если же канал искажает некоторые частоты из данного диапазона, то и весь сигнал на выходе канала будет искажённым. Тогда канал будет выполнять функции так называемого фильтра – он будет пропускать неизменными лишь часть синусоид исходного сигнала. Иногда это полезно, когда нам самим требуется исказить передаваемый сигнал, например, когда для целей очистки исходного сигнала от посторонних шумов требуется подавить некие лишние синусоиды, которые и являются мешающими шумами.
       Есть и другие интересные области применения спектрального представления сигналов. Например, известна методика спектрального анализа. Для того чтобы выяснить состав исследуемого нами вещества, мы заставляем излучать данное вещество нагрев его до определённой температуры. Далее это излучение проходит через набор специальных призм и таким образом определяется амплитудный спектр полученого излучения. У каждого химического элемента свой амплитудный спектр его излучения, отсюда поняв, на что похож спектр исследуемого нами вещества, можно определить его химический состав. Кстати, тут сразу становится очевидной интересная задача, которая не решена до сих пор (на момент начала 2014 г.). Мы можем легко определить амплитудный спектр излучения вещества, но из вышеизложенного нам известно, что для полного описания данного излучения (данных колебаний, которые выдаёт нагретое вещество) необходимо знать ещё и его фазовый спектр. Тогда по амплитудному и фазовому спектру при помощи формулы (2) мы смогли бы полностью восстановить “сигнал”-колебание, которое излучает данное вещество. Повторюсь, только по амплитудному спектру восстановить этот “сигнал” (это колебание) нельзя. А вот по амплитудному и фазовому спектрам, повторюсь, мы смогли бы в точности восстановить то, как именно колеблются атомы вещества. Зная в точности то, как колеблется каждый химический элемент и как отличаются формы колебаний разных химических элементов друг от друга мы могли бы строить более обоснованные предположения о том, как устроены данные химические элементы вплоть до тонких особенностей этого строения, которые не известны до сих пор и знание которых позволило бы создавать новые материалы и вещества с ранее не виданными свойствами. В итоге решение задачи определения фазового спектра излучения вещества сулит немалую выгоду. Это к слову о нанотехнологиях. Таким образом, мы коснулись ещё одной области применения спектрального представления сигналов – это распознавание сигналов по их спектрам. В вышеприведённом примере мы при помощи амплитудного спектра отличаем друг от друга сигналы (излучения) тех или иных веществ, а значит, по спектру сигнала распознаём вещество, с которым в данный момент имеем дело.
       Существуют и другие задачи распознавания сигналов решаемые при помощи спектров. Можно, например, по некоторым особенностям амплитудного спектра голосового сигнала определить принадлежит ли данный голосовой сигнал данному человеку с таким-то голосом. То есть этот ли человек сообщил, например, в полицию о заложенной бомбе или нет. А всё потому, что у каждого человека есть свои индивидуальные особенности спектра его речевого сигнала. То есть по записи телефонного сообщения определяем амплитудный спектр и далее, заставив подозреваемого человека произнести то же сообщение, что и на записи, находим амплитудный спектр и этого образца сигнала. Сравниваем спектр телефонной записи со спектром свежей записи голоса подозреваемого. Если спектры по определённым критериям совпадают, то мы нашли того, кто сообщал о бомбе по телефону. Существуют способы определения спектров для изображений, фотографий (тут используются уже двумерные спектры в отличии от одномерных, которые мы рассмотрели только что) и т.д. В итоге по особенностям спектра изображения можно определять есть ли на данном изображении те или иные объекты – это ещё один из примеров решения задачи автоматического распознавания при помощи спектров. Существует также множество разнообразных примеров, где представление сигнала S(t) в виде суммы простейших колебаний помогает в решении самые разных задач в том числе и в таких областях, как системы связи, информационные и компьютерные технологии, финансы и др.
       К слову сказать, дальнейшее развитие идеи синтеза из простейших сигналов более сложных (попытка представить сложный сигнал в виде суммы простых) – есть попытка в качестве базовых “кирпичиков” применять не синусоиды, а какие-либо другие простейшие сигналы. Именно это и лежит в основе вейвлет-анализа (см., например, здесь).

p.s. Для того, кто интересуется объяснениями понятий математики и физики что называется "на пальцах" можно посоветовать вот эту книгу и в частности главы из её разделов "Математика", "Физика" (саму книгу или отдельные главы из неё вы можете приобрести здесь).

Обсудить на форуме

ПРЕДЫДУЩАЯ СТРАНИЦА ИСХОДНАЯ СТРАНИЦА

Комментарии