Категории:
Суть фильтра Калмана
Этот фильтр применяют в разных областях – от радиотехники до экономики. Здесь мы обсудим основную идею, смысл, суть данного фильтра. Излагаться она будет максимально простым языком.
Предположим, что у нас есть необходимость в измерениях некоторых величин некоего объекта. В радиотехнике чаще всего имеют дело с измерениями напряжений на выходе некоего устройства (датчика, антенны и т.д.). В примере с электрокардиографом (см. здесь) мы имеем дело с измерениями биопотенциалов на теле человека. В экономике, например, измеряемой величиной могут быть курсы валют. Каждыё день курс валют разный, т.е. каждый день “его измерения” дают нам разную величину. А если обобщать, то можно сказать, что большая часть деятельности человека (если не вся) сводится именно к постоянным измерениям-сравнениям тех или иных величин (см. книгу).
Итак, предположим, что мы что-то постоянно измеряем. Так же предположим, что наши измерения всегда идут с некоторой ошибкой – оно и понятно, ведь нет идеальных измерительных приборов, и каждый выдаёт результат с ошибкой. В простейшем случае описанное можно свести к следующему выражению: z=x+y, где x – истинное значение, которое мы хотим измерить и которое измерили бы если бы у нас был идеальный измерительный прибор, y – ошибка измерения, вносимая измерительным прибором, а z – измеренная нами величина. Так вот задача фильтра Калмана состоит в том, чтобы по измеренной нами z всё-таки догадаться (определить), а какое же истинное значение x было, когда мы получали нашу z (в которой "сидит" истинное значение и ошибка измерения). Необходимо отфильтровать (отсеять) из z истинное значение x – убрать из z искажающий шум y. То есть, имея на руках только лишь сумму нам необходимо догадаться о том, какие слагаемые дали эту сумму.
В свете вышеописанного сформулируем теперь всё следующим образом. Пусть есть всего лишь два случайных числа. Нам даётся только их сумма и от нас требуется по этой сумме определить, какими являются слагаемые. Например, нам дали число 12 и говорят: 12 – это сумма чисел x и y, вопрос – чему равны x и y. Чтобы ответить на этот вопрос, составляем уравнение: x+y=12. Мы получили одно уравнение с двумя неизвестными, поэтому, строго говоря, найти два числа которые и дали эту сумму не возможно. Но кое-что об этих числах мы всё-таки можем сказать. Мы можем сказать, что это были либо числа 1 и 11, либо 2 и 10, либо 3 и 9, либо 4 и 8 и т.д., также это либо 13 и -1, либо 14 и -2, либо 15 и -3 и т.д. То есть мы можем по сумме (в нашем примере 12) определить множество возможных вариантов, которые дают в сумме именно 12. Один из этих вариантов – это искомая нами пара, которая на самом деле прямо сейчас и дала 12. Нелишне так же отметить, что все варианты пар чисел дающих в сумме 12 образуют прямую, изображённую на рис.1, которая и задаётся уравнением x+y=12 (y=-x+12).
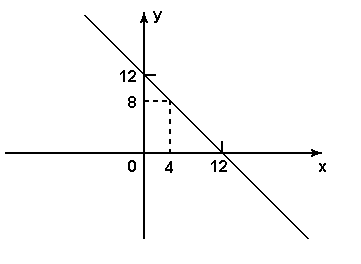
рис.1
Таким образом, искомая нами пара лежит где-то на этой прямой. Повторюсь, выбрать из всех этих вариантов ту пару, которая была на самом деле – которая дала число 12, не владея какими-либо дополнительными подсказками, невозможно. Однако, в ситуации, для которой изобретён фильтр Калмана, такие подсказки есть. Там заранее о случайных числах кое-что известно. В частности там известна так называемая гистограмма распределения для каждой пары чисел. Она обычно бывает получена после достаточно длительных наблюдений за выпадениями этих самых случайных чисел. То есть, например, из опыта известно, что в 5% случаев обычно выпадает пара x=1, y=8 (обозначим эту пару так: (1,8)), в 2% случаев пара x=2, y=3 (2,3), в 1% случаев пара (3,1), в 0.024% случаев пара (11,1) и т.д. Повторюсь, эта гистограмма задана для всех пар чисел, в том числе и для тех, что образуют в сумме 12. Таким образом, для каждой пары, что даёт в сумме 12, мы можем сказать, что, например, пара (1, 11) выпадает в 0.8% случаев, пара (2, 10) – в 1% случаев, пара (3, 9) – в 1.5% случаев и т.д. Таким образом, мы можем по гистограмме определить, в скольких процентах случаев сумма слагаемых пары равна 12. Пусть, например, в 30% случаев сумма даёт 12. А в остальных 70% выпадают остальные пары – это (1,8), (2,3), (3,1) и т.д. – те, что в сумме дают числа отличные от 12. Причём пусть, например, пара (7,5) выпадает в 27% случаев в то время, как все остальные пары, что дают в сумме 12, выпадают в 0.024%+0.8%+1%+1.5%+…=3% случаев. Итак, по гистограмме мы выяснили, что числа дающие в сумме 12 выпадают в 30% случаев. При этом мы знаем, что если выпало 12, то чаще всего (в 27% из 30%) причиной этого является пара (7,5). То есть если уже выпало 12, то мы можем сказать, что в 90% (27% из 30% – или, что то же самое 27 раз из каждых 30-ти) причиной выпадения 12 является пара (7,5). Зная, что чаще всего причиной получения суммы равной 12 является пара (7,5) логично предположить, что, скорее всего, она выпала и сейчас. Конечно, всё-таки не факт, что на самом деле сейчас число 12 образовано именно этой парой, однако, в следующие разы, если нам попадётся 12, и мы опять предположим пару (7,5), то где-то в 90% случаев из 100% окажемся правы. А вот если мы будем предполагать пару (2, 10), то окажемся правы лишь в 1% из 30% случаев, что равно 3.33% правильных догадок по сравнению с 90% при предположении пары (7,5). Вот и всё – в этом и состоит смысл алгоритма фильтра Калмана. То есть фильтр Калмана не гарантирует, что не ошибётся в определении слагаемого по сумме, однако он гарантирует, что ошибётся минимальное количество раз (вероятность ошибки будет минимальна), так как использует статистику – гистограмму выпадения пар чисел. Так же необходимо подчеркнуть, что часто в алгоритме фильтрации Калмана используется так называемая плотность распределения вероятности (ПРВ). Однако необходимо понимать, что смысл там тот же, что и у гистограммы. Более того, гистограмма – это функция, построенная на основе ПРВ и являющаяся её приближением (см., например, здесь).
В принципе мы эту гистограмму можем изобразить в виде функции двух переменных – то есть в виде некоей поверхности над плоскостью xy. Там, где поверхность выше, там выше и вероятность выпадения соответствующей пары. На рис.2 изображена такая поверхность.
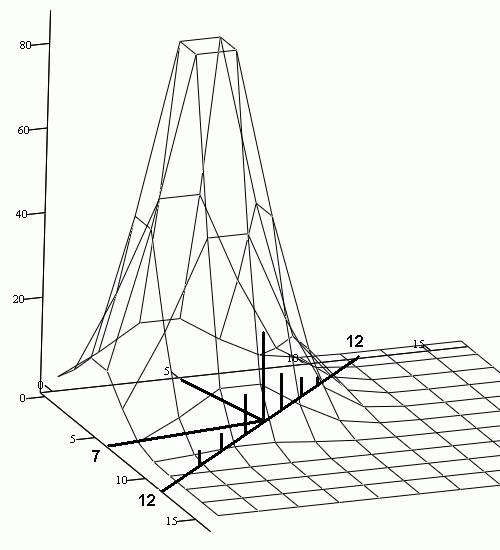
рис.2
Как видно над прямой x+y=12 (которая есть варианты пар дающих в сумме 12) расположены точки поверхности на разной высоте и наибольшая высота у варианта с координатами (7,5). И когда нам встречается сумма равная 12, в 90% случаев причиной появления этой суммы является именно пара (7,5). Т.е. именно эта пара, дающая в сумме 12, имеет наибольшую вероятность появления при условии, что сумма равна 12.
Таким образом, здесь описана идея лежащая в основе фильтра Калмана. Именно на ней и построены всевозможные его модификации – одношаговые, многошаговые рекуррентные и т.д. Для более глубокого изучения фильтра Калмана рекомендую книгу: Ван Трис Г. Теория обнаружения, оценок и модуляции.
p.s. Для того, кто интересуется объяснениями понятий математики что называется "на пальцах" можно посоветовать вот эту книгу и в частности главы из её раздела "Математика" (саму книгу или отдельные главы из неё вы можете приобрести здесь).
Комментарии
Следователь
22/12/15 16:22
Константин ! А почему Вы не рассматриваете использование нейронных сетей для проектирования фильтров известных в настоящее время и тех , которые будут изобретены в ближайшее время ? Ведь любой фильтр - это частный случай применения нейронных сетей ! Зачем тратить время на частности , когда можно потратить его на изучение методики , позволяющей спроектировать любую частность ? Что думаете по этому поводу ?
Следователь
22/12/15 16:31
Аппроксимация частотных характеристик цифровых фильтров с помощью нейронных сетей http://matlab.exponenta.ru/conf2002/thesises/section4/sautov/sautov.php
Следователь
22/12/15 16:33
Требования к точности проектирования фильтров СВЧ высоки и, ло-видимому, во многих случаях могут быть удовлетворены только в рамках многомерного электродинамического анализа. Поэтому весьма актуальным является ислользование такого подхода к проектированию, который бы обеспечивал высокую точность при небольших затратах временных и вычислительных ресурсов. Одним из таких подходов является использование технологии «визуального» проектирования, реализованной в системе . Предварительно строится нейронная модель фильтра . http://nauchebe.net/2013/02/vizualnoe-proektirovanie-filtrov-svch-na-osnove-nejronnyx-modelej/
Константин
22/12/15 17:22
Нейронная сеть обученная на примерах может оказаться не точной по сравнению, например, с тем же фильтром Калмана построенного под конкретные условия. Так как набор примеров для обучения сети может оказаться не полным.
Следователь
22/12/15 17:27
Ну тут будет виновата не концепция нейронных сетей , а тот , кто ей в недостаточной степени владеет. В определенной степени это искусство. Но очень перспективное.
Константин
22/12/15 17:30
Вот именно, пока что люди не умеют подбирать параметры нейронной сети кроме обучения её на примерах, а тут уже велика вероятность ошибки. Нет выверенных точных методик подбора обучающего набора примеров и пока даже это на уровне искусства.
DZ
05/10/20 13:05
Боже, что за бред здесь написан?? Автор, похоже, в принципе не представляет работу фильтра Калмана.
Константин
05/10/20 15:59
Что вам конкретно не понятно?
