Категории:
Просто о сигналах и спектрах (продолжение)
Мы начали рассматривать сигналы на примере системы связи, где есть передающая сторона (источник информации и сигналов), приёмная сторона (куда должны прийти сигналы от передающей стороны) и канал связи (среда или техническое устройство где передаются-распространяются сигналы от передающей стороны к приёмной). Сигналы, как мы выяснили это часто довольно изощрённые колебания. Итак, при передаче, например, музыки или речи необходимо заставить пластину на приёмной стороне (см. про пластину здесь) совершать довольно сложные колебания – те же колебания, что совершает подобная пластина на передающей стороне. Передаются эти колебания при помощи канала связи. В канале связи для этого вызываются соответствующие колебания электрического тока.
В процессе в том числе и совершенствования систем связи оказалось, что было бы удобно научиться как-то описывать довольно сложные колебания который мы передаём при помощи нашей системы связи. Стало необходимым научиться измерять колебательные характеристики этих самых сложных колебаний, например, для того чтобы выяснять – подойдёт ли, например, такой-то лист железа для воспроизводства таких-то колебаний (см. про колебания от железной пластины здесь) – сможет ли, например, данная мембрана на приёмной стороне идеально воспроизвести необходимые нам колебания или исказит их так, что мы на приёмной стороне получим совсем не то, что пытались передать по каналам связи. А ещё бывает, что и канал связи не сможет передать все тонкости колебательного процесса, что имеется на передающей стороне и тогда нам надо для таких сложных колебаний применять другой канал связи. В связи с этим есть необходимость изучать характеристики колебаний, а для этого хорошо бы научиться их как-то описывать.
Ну и как описать довольно сложный колебательный процесс? Здесь самая первая идея – это попытаться сложный колебательный процесс представить в виде набора простых колебательных процессов. Так же как и везде – мы сложный объект или движение пытаемся представить в виде совокупности неких более простых, базовых "кирпичиков". То же и в описании сложного колебательного процесса. И оказывается, что человечество довольно давно обнаружило простейшие колебания при помощи которых можно строить более сложные колебания. Это обыкновенные звуковые тоны. В простейшем случае тон это то, что даёт каждая струна музыкального инструмента. Каждая струна даёт свой тон. И при помощи этих простейших колебаний-звуков (тонов) можно создавать более сложные колебания-звуки – музыку. То есть более изощрённое колебание это всего лишь сумма простейших тонов. Потом оказалось, что любой колебательный процесс (в том числе и человеческая речь и вообще любые звуки, что мы слышим) можно представить в виде суммы этих самых простейших колебаний-тонов. А потом выяснилось, что не только колебательные, но и любые движения мембраны можно представить в виде суммы простейших "тонов". Так же, выяснилось, что в виде суммы "тонов" могут быть представлены не только звуковые сигналы, но и любые другие сигналы: оптические, телевизионные, радиолокационные и т.д. Собственно в этом и суть спектра. Спектр для данного сигнала это и есть такое описание, где указаны все "тона" и их характеристики, которые необходимо взять чтобы из этих "тонов" получить данный сигнал. Рассмотрим теперь всё это поподробнее.
Итак, как уже сказано, сочетая некие базовые колебания можно создавать более сложные. Собственно идея такая. Представим некий рояль, а ещё лучше современный синтезатор звуков. У этого синтезатора есть множество клавиш при нажатии на каждую издаётся свой простейший звук (тон) – генерируется своё простейшее колебание (в данном случае колебание динамика, а вместе с ним и воздуха). Разные клавиши дают разные простейшие колебания. Причём пусть у нас синтезатор устроен так, что чем сильнее мы жмём на клавишу, тем громче звук. Если мы одновременно нажмём, например, пять разных клавиш с разной силой и будем удерживать их нажатыми, например, три минуты не меняя силу нажатия, то в течение этих трёх минут будем слышать некий постоянный сложный звук. Повторим эксперимент – опять в течении трёх минут удерживаем нажатыми те же самые клавиши, но сила нажатия на каждую клавишу теперь другая нежели в первом эксперименте. В итоге во втором эксперименте в течении трёх минут мы будем слышать уже другой результирующий звук от синтезатора. Таким образом, мы можем конструировать самые разные звуки. То есть из простейших колебаний можем конструировать разные сложные колебания. Конкретизируем теперь описанное при помощи математики.
Пусть синтезатор устроен так, что каждый простейший звук (тон) каждой клавиши это синусоидальное колебание со своей частотой. То есть нажатие на клавишу вызывает колебание воздуха, а в месте с ним и колебание перепонки нашего уха так, что если по оси X мы отложим время, а по оси Y положение перепонки уха относительно её спокойного состояния, то в итоге получим график синусоиды (см. рис.7 – сгенерировано при помощи системы Matcad). Также чем сильнее мы жмём на клавишу, тем больше амплитуда соответственно синусоиды – тем с большим размахом колеблется перепонка нашего уха и тем громче мы слышим звук. На рис.7 и рис.8 представлены синусоиды с разными амплитудами.
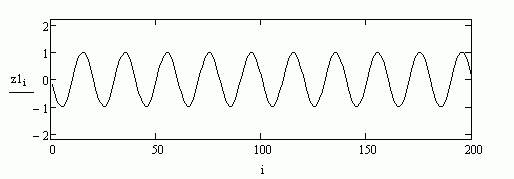
рис.7
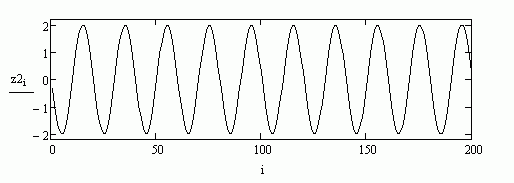
рис.8
На рис. 9 представлена синусоида, получаемая при нажатии на другую клавишу в отличие от рис.7, рис.8. Т.е. на рис. 9 у нас синусоида с другой частотой.
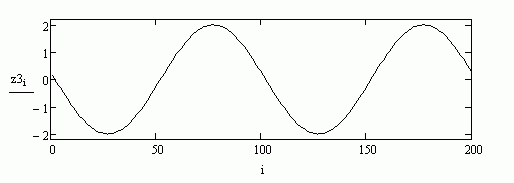
рис.9
Итак, звуки от двух разных клавиш – это синусоиды с разными частотами. Каждая клавиша синтезатора даёт своё колебание (динамика, воздуха) в виде синусоиды со своей частотой. Кстати говоря, услышать то, как звучит синусоидальное колебание с частотой 440 Гц (440 максимумов в секунду) можно достаточно просто: поднесите к уху трубку стационарного телефона и вы услышите непрерывный звук (тон). Этот звук и есть колебания с частотой 440 Гц. Когда мы на нашем синтезаторе непрерывно жмём одновременно на две клавиши, то получаем две синусоиды, которые складываются-суммируются. На рис.12 изображён график суммы двух синусоид с рис. 10.
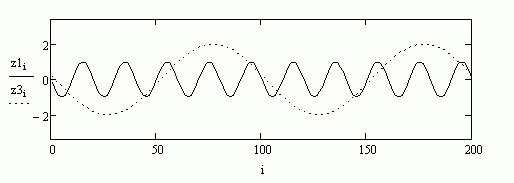
рис.10
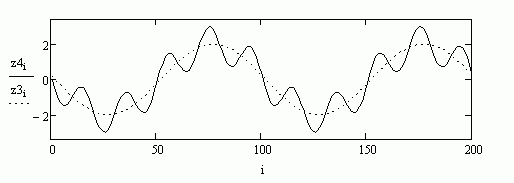
рис.11
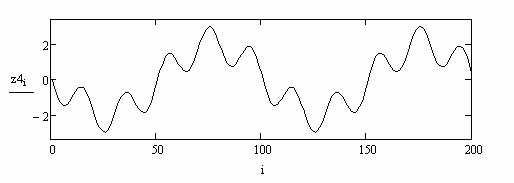
рис.12
На рис. 13 изображена сумма 3-хсинусоид. На рис.14 сумма трёх синусоид с теми же частотами, но другими амплитудами. Как видим суммарный график рис. 14 отличается от суммарного графика рис.13. И это несмотря на то, что частоты трёх простейших синусоид не изменились (поменяли мы лишь их амплитуды – силу нажатия на каждую клавишу, а сами клавиши те же).
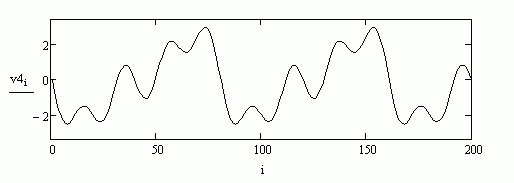
рис.13
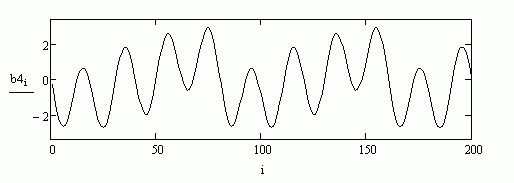
рис.14
Таким образом, мы можем нажимать сочетания клавиш и удерживать их с разной силой в течение, например, трёх минут и каждый раз будем получать в течение этих трёх минут разные суммарные звуки-колебания. Таким образом, перед нами открывается возможность конструирования разных звуков при помощи одних и тех же “кирпичиков” – одних и тех же клавиш (одних и тех же простейших колебаний-синусоид, но с разными амплитудами). Пусть у нашего синтезатора этих клавиш, например, 10 тысяч – то есть это 10 тысяч синусоид с разными частотами. Вопрос: можем ли мы подобрав всего лишь правильно силу нажатия на каждую клавишу нашего синтезатора (всего лишь подобрав правильно амплитуды синусоид) сконструировать любой звук, в том числе и звук человеческого голоса при произнесении человеком какого-либо слова? Чтобы ответить на этот вопрос необходимо понять следующее: влияет ли на вид получаемого звука что-то ещё кроме силы нажатия на клавиши? Ответ – да, есть ещё фактор, который позволяет менять суммарный звук, даже если каждый раз мы нажимаем одни и те же клавиши с той же силой, что и в предыдущие разы. Фокус тут следующий. Изначально мы предполагали, что все клавиши нажимаются одновременно. Однако, пусть клавиши нажимаются не одновременно, а с некоторой задержкой относительно момента нажатия самой первой клавиши. И пусть три минуты времени звучания суммарного звука мы будем отсчитывать только с момента нажатия последней клавиши. Тогда синусоиды от разных клавиш будут отличаться не только частотами и амплитудами, но будут ещё и сдвинуты по времени друг относительно друга. На рис. 15 приведены две синусоиды без сдвига друг относительно друга и их сумма.
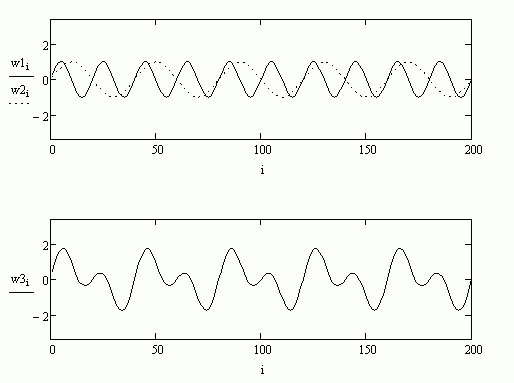
рис.15
На рис.16 приведены две синусоиды сдвинутые друг относительно друга (начало одной мы задержали относительно другой) и их сумма.
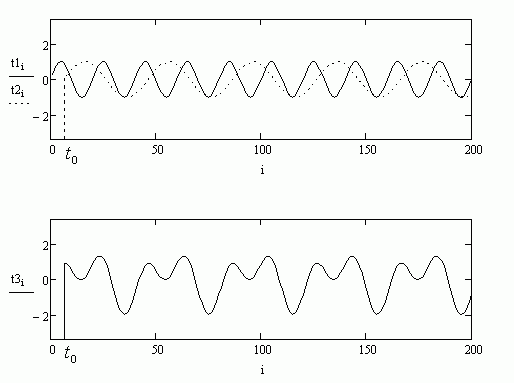
рис.16
В итоге суммарный график на рис.16 отличается от суммарного графика на рис.15. Таким образом звук суммы синусоид с того момента как нажаты обе клавиши синтезатора на рис.16 (с момента
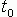) отличается от звука суммы синусоид рис.15.
Так вот оказалось, что если подобрать нужным образом не только амплитуды каждой синусоиды, но и сдвиги синусоид по времени (задержки) относительно некоего стартового момента общего для всех, то таким образом можно на нашем синтезаторе сгенерировать любой звук-колебание любой формы, в том числе и звук человеческого голоса произносящего какое-либо слово.
То есть если нажать с нужной силой и в нужные моменты времени клавиши нашего синтезатора, то в итоге можно сгенерировать любой звук-колебание-сигнал. Всё это напоминает обычную игру на рояле, где человек должен лишь вовремя и с нужной силой нажимать соответствующие клавиши инструмента.
Главное чтобы у нашего рояля-синтезатора было достаточно клавиш. Например, известно, что звук человеческого голоса располагается в диапазоне от 50 до 10000 Гц (см., например, здесь). Это означает, что для генерирования звуков человеческого голоса потребуется синтезатор с как минимум 9950 клавишами
(ведь нам могут потребоваться и клавиши с не целыми частотами – тогда клавиш потребуется больше, чем 9950).
Каждая клавиша будет выдавать синусоиду со своей частотой. И теперь если у нас такой синтезатор есть, то для того чтобы сгенерировать звук голоса, например, человека по имени Вася, произносящего слово “самолёт” нужно подобрать силу нажатия на каждую клавишу этого синтезатора, а так же задержки с которыми эти клавиши будут нажаты друг относительно друга.
Если мы сможем эти силы и эти задержки соблюсти, то получим нужный нам звук. Для другого слова произносимого тем же Васей нужны другие силы нажатия и задержки.
Математически это можно сформулировать так: необходимо знать амплитуду каждой синусоиды и её сдвиг по времени относительно других синусоид (ну или относительно какого-то общего стартового момента времени) для того чтобы сумма этих синусоид дала нужный нам сигнал S(t). В виде формулы записать это можно следующим образом:
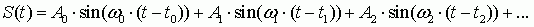
где
, 
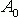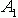и т.д. – амплитуды синусоид (соответствуют силе нажатия на каждую клавишу), 
, 
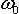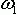– частоты синусоид, 
, 
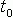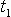– сдвиги синусоид по оси времени относительно начала координат (соответствуют времени нажатия на каждую клавишу).
ПРЕДЫДУЩАЯ СТРАНИЦА СЛЕДУЮЩАЯ СТРАНИЦА
Комментарии
