Категории:
Здесь разъясняется основной принцип оцифровки
Оцифровка – это описание какого-либо объекта в виде набора чисел. В компьютере информация может быть записана только числами, а точнее в виде комбинаций чисел: 0 и 1. Таким образом, прежде чем записать какую-либо информацию в компьютер её нужно зашифровать, закодировать последовательностью нулей и единиц – оцифровать. Сами 0 и 1 записаны в компьютере не в виде чёрточек-следов на бумаге, как это делаем мы. В компьютере 0 и 1 хранятся в виде следов другого типа: например, если внутри жесткого диска (винчестера) определённый его участок намагничен, значит там записана 1, участок не намагничен – там записан 0. Если мы, например, хотим записать в компьютер информацию о том, как менялось электрическое поле на теле человека в течении такого-то времени (в нашем случае это электрокардиограмма), то и эту информацию мы должны сначала перевести в последовательность нулей и единиц – то есть оцифровать. Как известно процесс изменения чего-то во времени (в нашем случае – электрического поля на теле) можно представить в виде графика, где по оси X будет откладываться время, по оси Y величина этого поля. Так вот, непрерывный график изменения чего-либо обычно называют аналоговым сигналом (подробнее о сигналах можно так же посмотреть здесь). После того, как сигнал закодируют последовательностью нулей и единиц, эту самую последовательность нулей и единиц называют цифровым сигналом. Устройство для перевода аналогового сигнала в цифровую форму называют аналогово-цифровым преобразователем (АЦП). АЦП просто делает замеры постоянно меняющегося напряжения электрического поля через определённые промежутки времени. Иными словами – АЦП измеряет значения сигнала через определённый промежутки времени. Каждое измеренное значение сигнала затем кодируется определённой последовательностью нулей и единиц по правилу, оговоренному в соответствующих госстандартах (ГОСТ-ах). Вот и весь основной принцип.
Если вы захотите восстановить из цифровой последовательности нулей и единиц исходный непрерывный (аналоговый сигнал), то тогда вы можете раскодировав эти последовательности выяснить, что когда-то АЦП измерив напряжение получил сначала, например, 0.3В, затем через одну тысячную секунды АЦП опять измерил напряжение и получил, например, 0.5В и т.д. Раскодировав нули и единицы вы получите, таким образом, всю историю измерений вашим АЦП напряжений. Но тут возникает вопрос: мы будем знать, что измерил АЦП в первую миллисекунду, будем знать, что он намерял во вторую миллисекунду и т.д., но например, будем ли мы знать каков был сигнал между 1-й и 2-й миллисекундой. Будем ли мы знать, каким был сигнал на 1.5 миллисекунде? Ответ прост: строго говоря, нет, так как цифровой сигнал – это запись информации о величине напряжений лишь в определённые моменты времени. Что было между этими моментами – в цифровом сигнале эта информация не содержится. Поэтому чтобы полностью восстановить каким аналоговый сигнал был в каждый момент времени, для этого применяют, так называемую, процедуру аппроксимации того или иного вида. Например, линейная аппроксимация изображена на рис.1a.
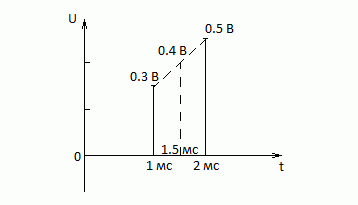рис.1a
Здесь мы, проведя прямую линию, соединяющую значения напряжения на 1-й миллисекунде и 2-й миллисекунде можем прикинуть, что было на 1.5-й и любой другой миллисекунде. Именно прикинуть, так как реальность может на самом деле отличаться от нашей прикидки. Тогда будет иметь место ошибка аппроксимации. Таким образом, аппроксимация не гарантирует точного восстановления сигнала, хотя и даёт часто достаточно хорошее приближение. Кстати, слово аппроксимация переводится именно как приближение. Так же необходимо подчеркнуть, что в реальных системах восстановления аналогового сигнала из цифрового чаще всего используется другой вид аппроксимации, нежели изображённый на рис.1a . Но и там применяется именно аппроксимация.
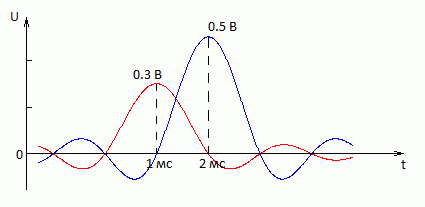рис.2а
Устройство, восстанавливающее аналоговый сигнал на основе цифрового называется цифро-аналоговым преобразователем (ЦАП). В ЦАП каждый отсчёт заменяется специальной sinc-функцией с амплитудой соотвествующей величине данного отсчёта. Сумма всех этих sinc-функций и даёт искомую аппроксимацию. На рис.2а и рис.2b изображён способ при помощи которого осуществляется аппроксимация в ЦАП для рис.1a. Здесь вместо отсчётов в 0.3В и 0.5В ставятся специальные sinc-функции амплитудой 0.3В и 0.5В соотвественно - см. рис.2а. А затем вычисляется сумма этих sinc-функций. Полученная сумма и даст искомую аппроксимацию – на рис. 2b сумма изображена пунктирной линией и, кстати, в момент времени 1.5 мс данная линия даёт значение 0.51В, а не так как на рис. 1a – 0.4В. Тут дело в том, что аппроксимация в ЦАП при определённых условиях (определяемых теоремой Котельникова) гораздо точнее линейной аппроксимации типа рис. 1a и соотвественно для одних и тех же моментов времени эти аппроксимации могут давать разные значения. Необходимо подчеркнуть, что если отсчётов не 2, как на рис.1a, а, например, 3 (или больше), то для вычисления аппроксимации нужно суммировать все 3 (и больше) sinc-функций. То есть для вычисления значения, например, в точке t = 1.5 мс нужно суммировать не только ближайшие sinc-функции c амплитудами 0.3В и 0.5В соотвественно, в точке t = 1.5 мс суммировать нужно все sinc-функции от всех отсчётов, которые образовали эти sinc-функции.
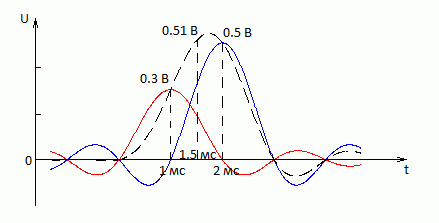рис.2b
Подробнее об аппроксимации применяемой в ЦАП можете посмотреть в литературе посвящённой теореме Котельникова.
p.s. Для того, кто интересуется объяснениями понятий математики, физики, техники что называется "на пальцах" можно посоветовать вот эту книгу и в частности главы из её разделов "Математика", "Физика", "Техника" (саму книгу или отдельные главы из неё вы можете приобрести здесь).
Комментарии
